Random Forest

Armani Harris, Amy Brown, Jeff Eddy

2023-07-31

Introduction

Random Forests (RF) is a popular ensemble learning algorithm that combines multiple decision trees to improve predictive accuracy and handle complex datasets. This literature review aims to explore ten articles that discuss various aspects of the Random Forest algorithm, including its theoretical foundation, feature selection, data imbalance resolution, interpretability, and comparisons with other classification methods. The selected articles offer valuable insights into the strengths, weaknesses, and practical applications of Random Forest in different domains.

Literature Review

Breiman (Breiman 2001)

  • Introduced the concept of Random Forests and highlighted the importance of the Law of Large Numbers in avoiding overfitting.

Liaw and Wiener (Liaw and Wiener 2002)

  • Expanded on this work, focusing on the classification and regression capabilities of RF.

Jaiswal, K. & Samikannu, R. (Jaiswal and Samikannu 2017)

  • Discussed the use of bagging and highlighted the significance of variable importance in RF models.When dealing with datasets containing a high number of variables the importance of feature selection.

Literature Review cont’d

Han and Kim (Han and Kim 2019) - Investigated the optimal size of candidate feature sets in Random Forest for classification and regression tasks.

  • The study reveals that the default candidate feature set is not always the best performing and that the optimal size can vary depending on the dataset used . The potential challenges such as overfitting and handling multi-valued attributes exist when using the Random Forest (RF) algorithm.

Abdulkareem, N. M., & Abdulazeez, A.(Abdulkareem and Abdulazeez 2021)

  • The advantages emphasized in this article entails accuracy, efficiency with large datasets, and minimal data preprocessing requirements.

Methods - Random Forest Algorithm

  • The algorithm consists of multiple uncorrelated un-pruned decision trees creating a forest.
  • The algorithm is a supervised learning model.
  • The algorithm can be used for both classification or regression models.
  • Two sampling methods reviewed: k-fold cross-validation and bootstrap.

Random Forest Decision Tree Structure

  • Root Node: Each tree starts with at a root node.
  • Internal Nodes: Each tree decision splits at the internal nodes using Gini Impurity or Permutation Importance for the feature importance.
  • Leaf Node: Each tree ends at the leaf node with the result stored as a categorical value for classification or numerical value for regression.
  • Final Result: The final result is calculated by taking the majority vote for classification or the average for regression (Abdulkareem and Abdulazeez 2021).

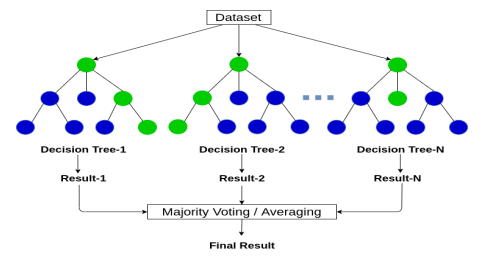
Figure 1 (Abdulkareem and Abdulazeez 2021)

Tree Decision Splits

  • Gini Impurity is calculated by summing the Gini decrease across every tree in the forest and divided by the number of trees in the forest to provide an average.
  • Permutation Importance is calculated by evaluating the decrease in accuracy when a feature is randomly shuffled over all trees in the forest (Jaiswal and Samikannu 2017).

Steps for Random Forest Algorithm

  • Step 1: Randomly select k features from a total of m features where k < m.
  • Step 2: Specify a node size d for the features selected in step 1 using the best split point discussed in step 3.
  • Step 3: Calculate the best split point at the internal node using Gini Impurity or Permuation Importance.
  • Step 4: Repeat the previous steps 1 through 3 until 1 node is remaining.
  • Step 5: Continue to build the forest by repeating all previous steps for n number of times to create n number of trees (Jaiswal and Samikannu 2017).

Dataset

  • Heart Disease Prediction dataset:
    https://www.kaggle.com/datasets/utkarshx27/heart-disease-diagnosis-dataset
  • 14 data fields (1 target and 13 features)
  • Target: Heart Disease - Predicting the presence or absence of heart disease
  • 270 observations
  • No missing values (Singh 2023)

Features and Target Fields

  • age
  • sex
  • chest pain type (4 values)
  • resting blood pressure
  • serum cholestoral in mg/dl
  • fasting blood sugar 120 mg/dl
  • resting electrocardiographic results (values 0, 1, 2)
  • maximum heart rate achieved
  • exercise induced angina
  • oldpeak = ST depression induced by exercise relative to rest
  • the slope of the peak exercise ST segment
  • number of major vessels (0-3) colored by flourosopy
  • thal: 3 = normal; 6 = fixed defect; 7 = reversable defect
  • heart disease (Target: (absence (1) or presence (2))
    (Singh 2023)

R Packages

  • caret package

    • Versatile package used for various classification and regression models.

    • Allows tuning of the model through parameters set in the package.

      • Parameter method set to rf for Random Forest algorithm.

      • Parameter trcontrol sets the sampling method for the dataset.

      • Parameter metric set to measure feature importance such as Accuracy and Gini Impurity (Johnson 2023).

  • dplyr package

    • Required for filtering dataframes and to produce the box plots of the data fields.

  • reshape2 package

    • Required to reshape the data to the correct format to build the box plots.

Visualization Box Plot #1

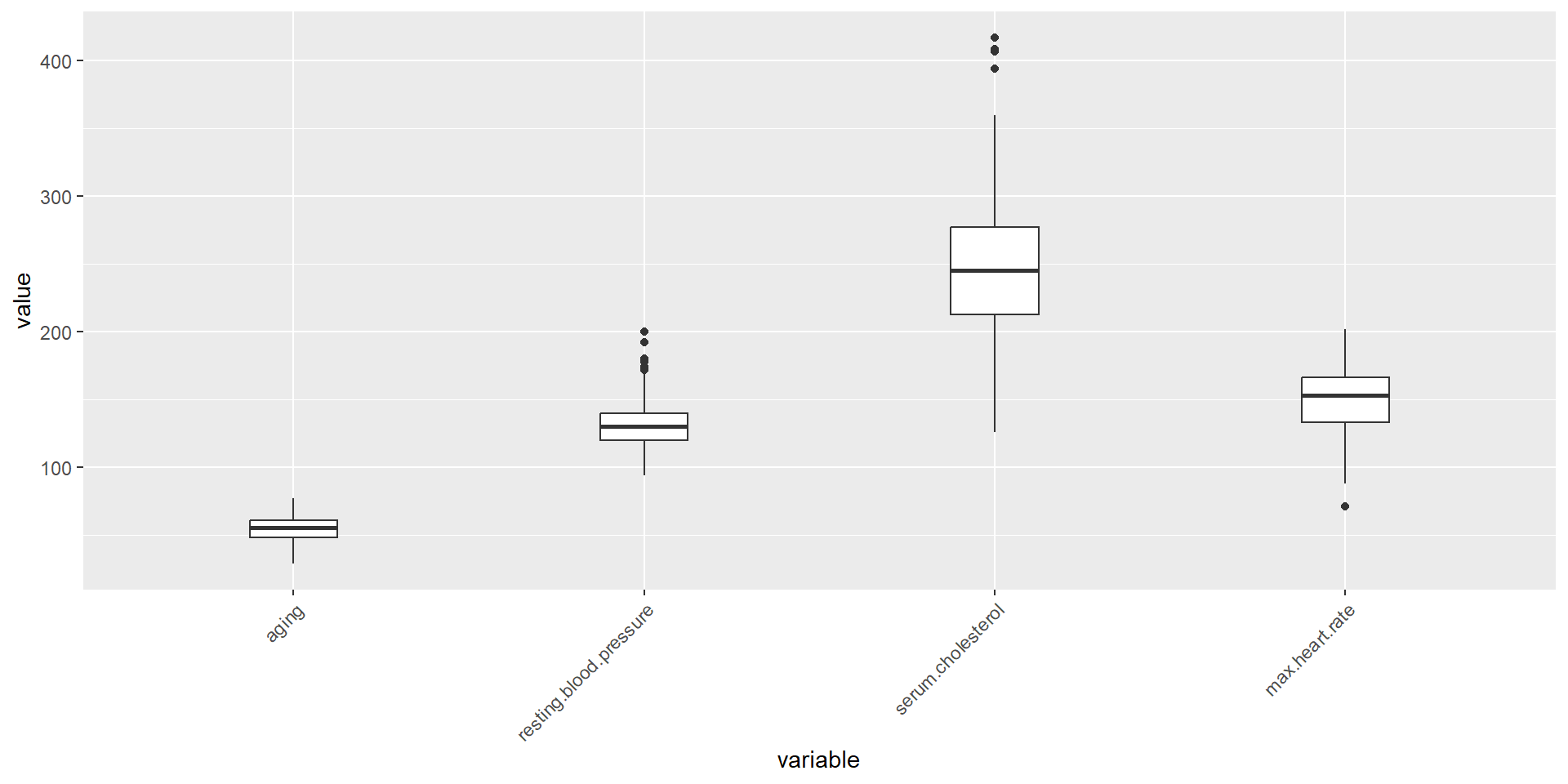
An extreme outlier was observed at a value of 564 in the feature serum cholesterol. Mild outliers were identified in features resting blood pressure, serum cholesterol, and max heart rate.

Visualization Box Plot #2

Mild outliers were identified in features chest pain type, fasting blood sugar, old peak, and major vessels.

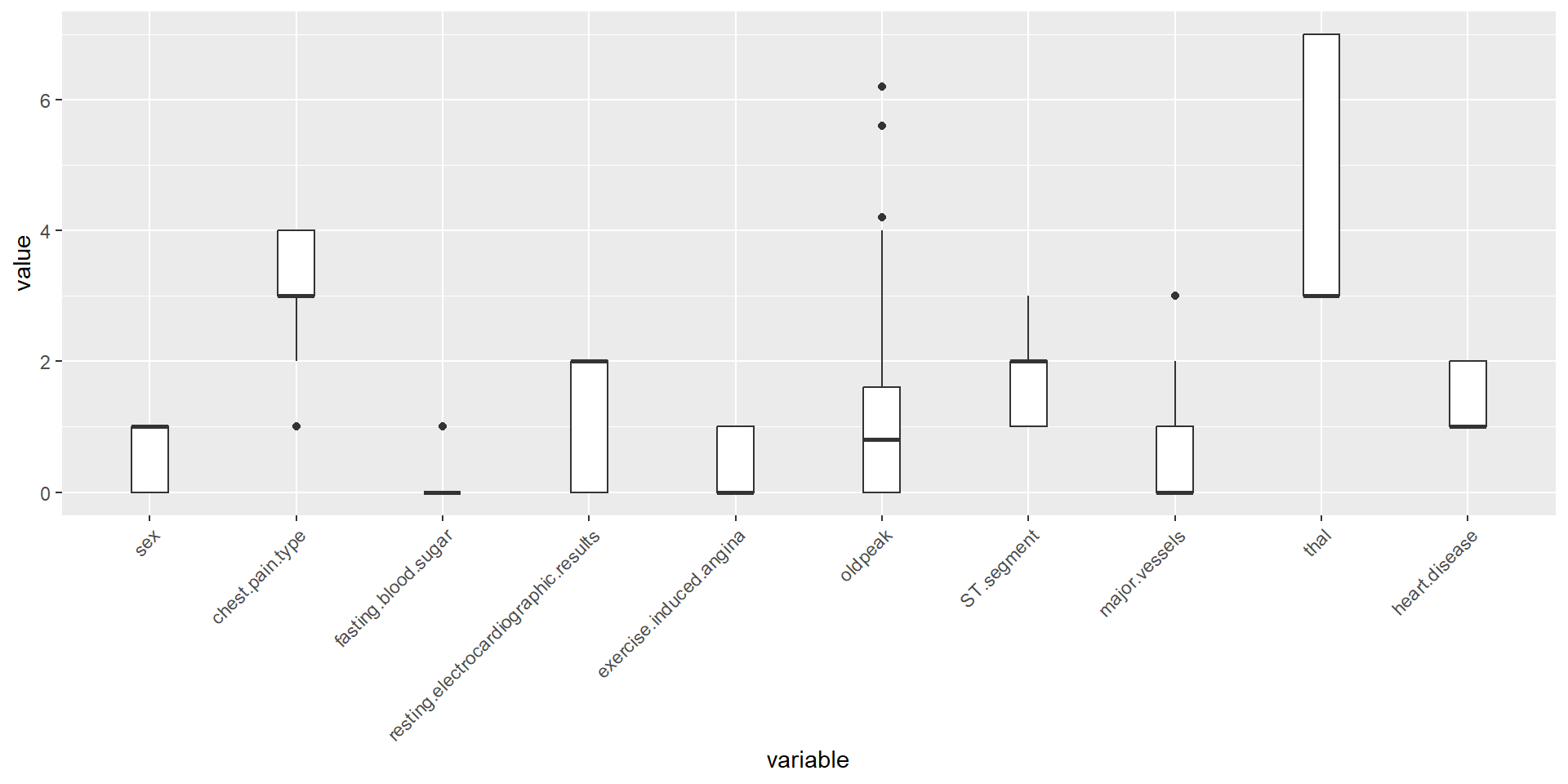
Removal of Extreme Outlier

Since the dataset is small, only the extreme outlier was removed. Box plot #1 was rerun to verify the extreme outlier of 564 was removed from feature serum cholesterol.

Data Transformation

  • Random forest classification model requires a dependent factor variable.
  • Target variable heart disease was transformed to a factor variable.

Model Training

The target variable was binary with categories of no heart disease (1) and heart disease (2).

  • 269 observations

  • Data set was split for a training model and a testing model at a 0.7 ratio.

  • 189 observations in the training data set and 80 in the testing data set.

K-Fold Cross-Validation: Default Training Model

  • 13 Predictor Features

  • 500 Decision Trees, 2 Features considered

  • Accuracy = 0.8358

Random Forest 

189 samples
 13 predictor
  2 classes: '1', '2' 

No pre-processing
Resampling: Cross-Validated (10 fold) 
Summary of sample sizes: 169, 170, 170, 171, 169, 171, ... 
Resampling results across tuning parameters:

  mtry  Accuracy   Kappa    
   2    0.8357895  0.6638724
   7    0.8311404  0.6531982
  13    0.8264035  0.6444556

Accuracy was used to select the optimal model using the largest value.
The final value used for the model was mtry = 2.

Bootstrap: Default Training Model

  • 13 Predictor Features

  • 500 Decision Trees, 2 Features considered

  • Accuracy = .8322

Random Forest 

189 samples
 13 predictor
  2 classes: '1', '2' 

No pre-processing
Resampling: Bootstrapped (25 reps) 
Summary of sample sizes: 189, 189, 189, 189, 189, 189, ... 
Resampling results across tuning parameters:

  mtry  Accuracy   Kappa    
   2    0.8321817  0.6571619
   7    0.8229013  0.6393790
  13    0.8117677  0.6172537

Accuracy was used to select the optimal model using the largest value.
The final value used for the model was mtry = 2.

Bootstrap Versus K-fold Cross-Validation

  • Bootstrap randomly selects n number of observations with replacement.

  • K-Fold Cross-validation creates subsets of the data then randomly shuffles the observations into the subset “folds”.

  • K-Fold trial was more accurate 0.8358 vs 0.8322.

K-Fold Cross-Validation: Tuning the Model

Selecting the best possible number of features first

Random Forest 

189 samples
 13 predictor
  2 classes: '1', '2' 

No pre-processing
Resampling: Cross-Validated (10 fold) 
Summary of sample sizes: 169, 170, 170, 171, 169, 171, ... 
Resampling results across tuning parameters:

  mtry  Accuracy   Kappa    
   1    0.8308187  0.6497031
   2    0.8521637  0.6938909
   3    0.8407895  0.6711918
   4    0.8410819  0.6746692
   5    0.8305556  0.6515543
   6    0.8311404  0.6546218
   7    0.8261404  0.6452077
   8    0.8150292  0.6223296
   9    0.8150292  0.6232846
  10    0.8047953  0.6038736

Accuracy was used to select the optimal model using the largest value.
The final value used for the model was mtry = 2.

K-Fold Cross-Validation: Optimal Number of Nodes


Call:
summary.resamples(object = results_mtry, metric = "Accuracy")

Models: 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 
Number of resamples: 10 

Accuracy 
        Min.   1st Qu.    Median      Mean   3rd Qu. Max. NA's
5  0.6842105 0.8355263 0.8947368 0.8674269 0.9000000    1    0
6  0.6842105 0.8355263 0.8947368 0.8674269 0.9000000    1    0
7  0.6842105 0.7807018 0.8210526 0.8360819 0.8947368    1    0
8  0.7368421 0.8355263 0.8460526 0.8624269 0.8986842    1    0
9  0.6842105 0.8355263 0.8460526 0.8519006 0.8947368    1    0
10 0.6842105 0.7921053 0.8377193 0.8363743 0.8815789    1    0
11 0.7368421 0.7938596 0.8421053 0.8463450 0.8835526    1    0
12 0.6842105 0.7833333 0.8421053 0.8413450 0.8855263    1    0
13 0.6842105 0.8355263 0.8421053 0.8521930 0.8835526    1    0
14 0.6842105 0.8083333 0.8421053 0.8521637 0.8986842    1    0
15 0.6842105 0.8355263 0.8421053 0.8569006 0.9000000    1    0

K-Fold Cross-Validation: Ideal Number of Trees


Call:
summary.resamples(object = results_tree, metric = "Accuracy")

Models: 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000 
Number of resamples: 10 

Accuracy 
          Min.   1st Qu.    Median      Mean   3rd Qu.      Max. NA's
100  0.7368421 0.7777778 0.8947368 0.8457895 0.8986842 0.9444444    0
200  0.7368421 0.7807018 0.8947368 0.8618713 0.9000000 1.0000000    0
300  0.6842105 0.8355263 0.8947368 0.8674269 0.9000000 1.0000000    0
400  0.6842105 0.8355263 0.8460526 0.8571637 0.8986842 1.0000000    0
500  0.6842105 0.8355263 0.8460526 0.8571637 0.8986842 1.0000000    0
600  0.6842105 0.8355263 0.8460526 0.8571637 0.8986842 1.0000000    0
700  0.6842105 0.8355263 0.8460526 0.8571637 0.8986842 1.0000000    0
800  0.6842105 0.8355263 0.8460526 0.8571637 0.8986842 1.0000000    0
900  0.6842105 0.8355263 0.8460526 0.8571637 0.8986842 1.0000000    0
1000 0.6842105 0.8355263 0.8460526 0.8571637 0.8986842 1.0000000    0

K-Fold Cross-Validation: Training the Final Model

  • 13 Predictor Features

  • 500 Decision Trees, 2 Features considered

  • Default Training Model Accuracy = 0.8358

Tuned Model uses:

  • 300 Trees

  • 6 nodes

  • 2 Features

  • Accuracy = .8674

Random Forest 

189 samples
 13 predictor
  2 classes: '1', '2' 

No pre-processing
Resampling: Cross-Validated (10 fold) 
Summary of sample sizes: 169, 170, 170, 171, 169, 171, ... 
Resampling results:

  Accuracy   Kappa    
  0.8674269  0.7242847

Tuning parameter 'mtry' was held constant at a value of 2

Bootstrap: Training the Final Model

Random Forest 

189 samples
 13 predictor
  2 classes: '1', '2' 

No pre-processing
Resampling: Bootstrapped (25 reps) 
Summary of sample sizes: 189, 189, 189, 189, 189, 189, ... 
Resampling results:

  Accuracy   Kappa    
  0.8344737  0.6605306

Tuning parameter 'mtry' was held constant at a value of 2

Final Model Comparison

  • K-Fold Cross-Validation Accuracy = .8674

  • Bootstrap Accuracy = .8345

  • Predictive Modeling will use K-Fold Cross-Validation due to higher accuracy

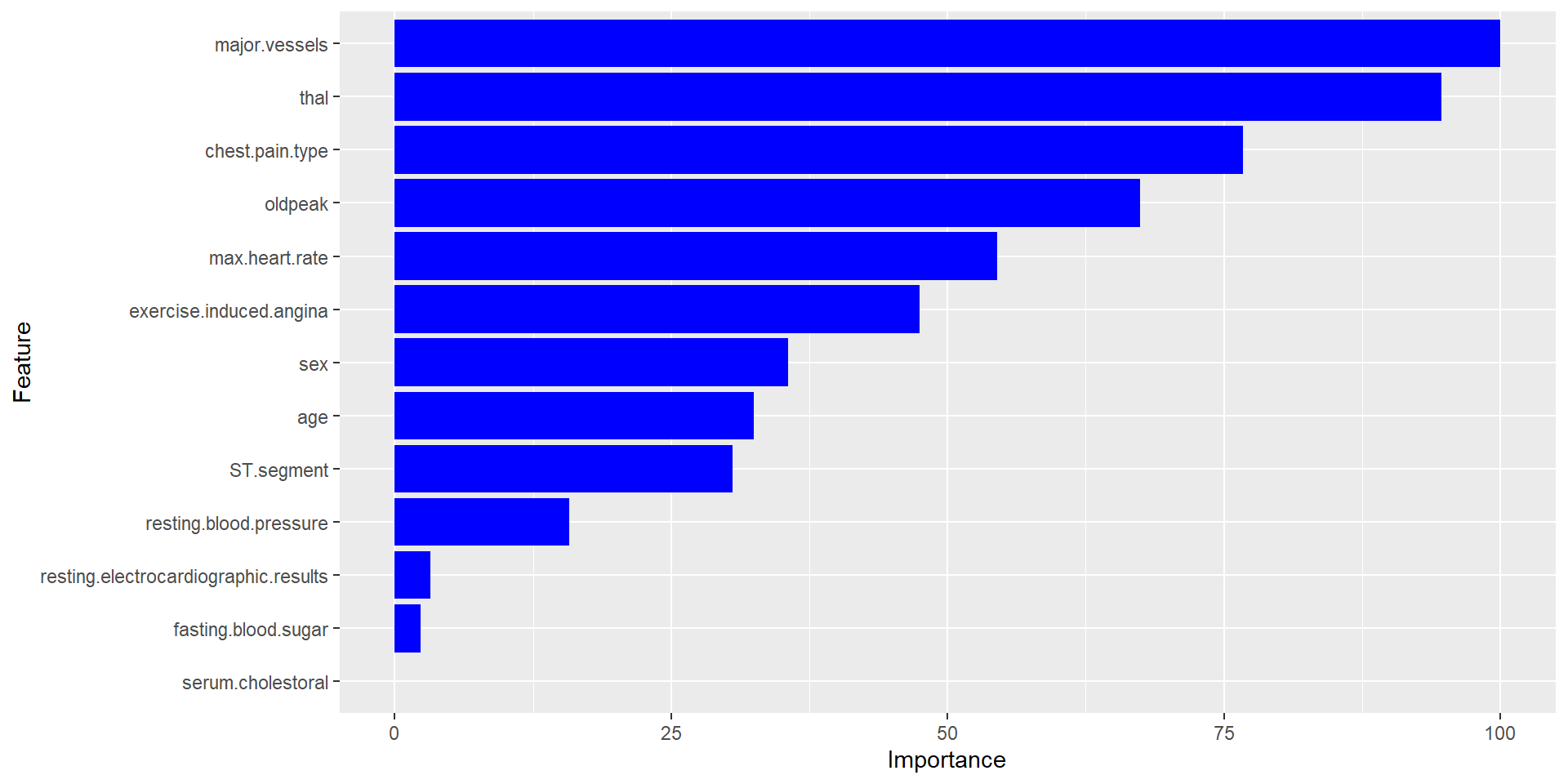
Predictive Modeling: Most Influential Features

  • Major Vessels

  • Thal

  • Chest Pain Type

  • Old Peak

  • Maximum Heart Rate

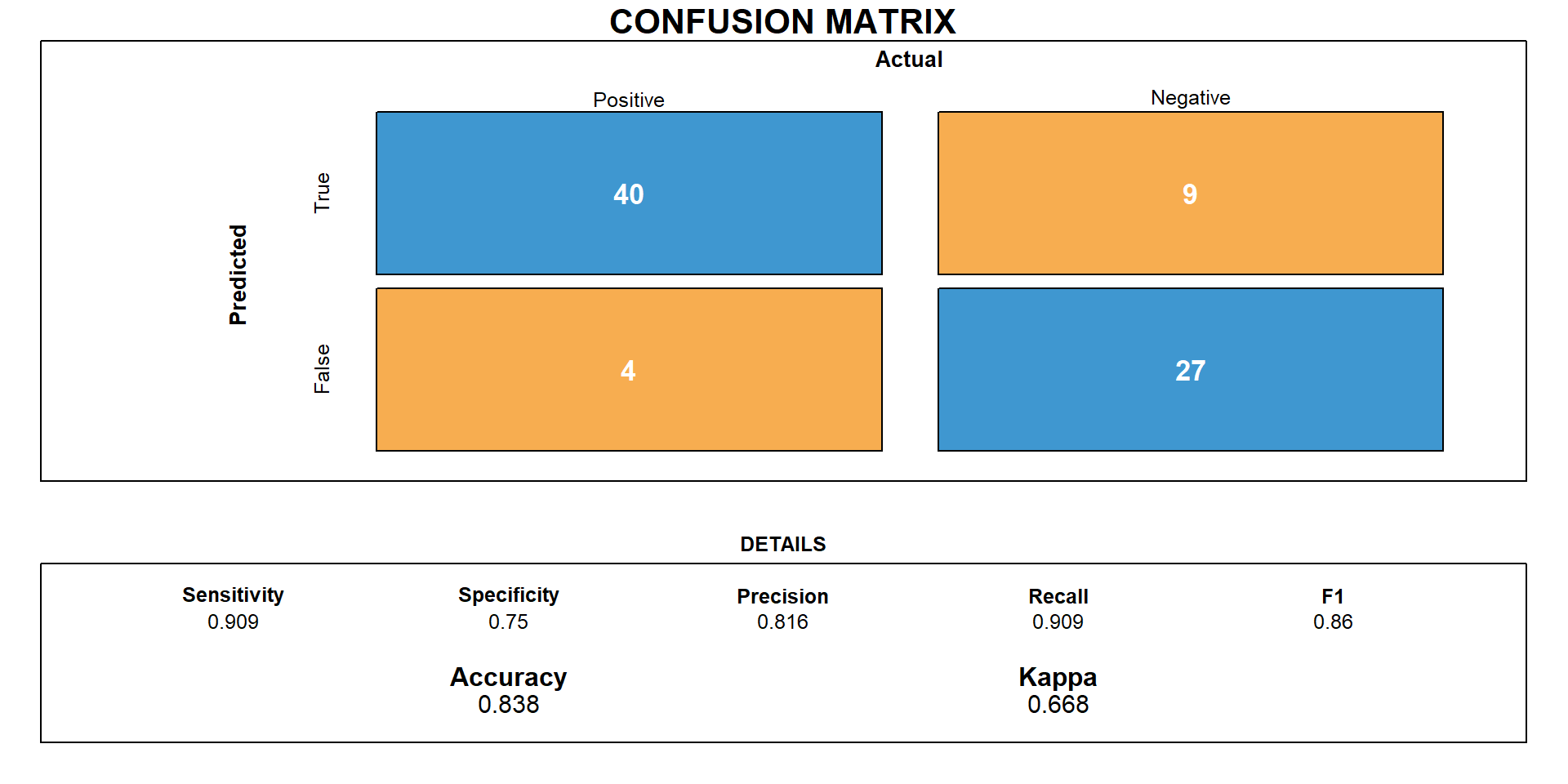
Predictive Model Accuracy

  • 83.8% (0.8375, CI: 0.7382, 0.9105, p< 0.001)

  • Sensitivity and specificity were calculated at 0.909 and 0.75 respectively

  • Estimated false positive rate of 30.77%

Conclusion

The Random Forest algorithm includes two feature sampling methods:

  • K-fold cross-validation

  • Bootstrap

The algorithm can be applied to both classification and regression tasks, with the prediction determined by the majority vote or average of the leaf nodes, respectively.

The algorithm is more cost effective and more reliable in understanding of the data.

Questions?

References

Abdulkareem, Nasiba Mahdi, and Adnan Mohsin Abdulazeez. 2021. “Machine Learning Classification Based on Radom Forest Algorithm: A Review.” International Journal of Science and Business 5 (2): 128–42.
Breiman, Leo. 2001. “Random Forests.” Machine Learning 45: 5–32. https://doi.org/10.1023/A:1010933404324.
Han, Sunwoo, and Hyunjoong Kim. 2019. “On the Optimal Size of Candidate Feature Set in Random Forest.” Applied Sciences 9 (5). https://doi.org/10.3390/app9050898.
Jaiswal, Jitendra Kumar, and Rita Samikannu. 2017. “Application of Random Forest Algorithm on Feature Subset Selection and Classification and Regression.” In 2017 World Congress on Computing and Communication Technologies (WCCCT), 65–68. https://doi.org/10.1109/WCCCT.2016.25.
Johnson, Daniel. 2023. “R Random Forest Tutorial with Example.” Guru99. https://www.guru99.com/r-random-forest-tutorial.html.
Liaw, Andy, and Matthew Wiener. 2002. “Classification and Regression by randomForest.” R News 2 (3): 18–22.
Singh, Utkarsh. 2023. “Heart Disease Prediction Dataset.” Kaggle. https://www.kaggle.com/datasets/utkarshx27/heart-disease-diagnosis-dataset.